Here were the challenges including my answers. The person playing teacher in this challenge says I got a B but since he's not documenting where I went wrong and telling me what the correct answers were my guess is he's just kind of making it up, so if we have a real teacher or professor in the house how did I really do on this and what were my mistakes?
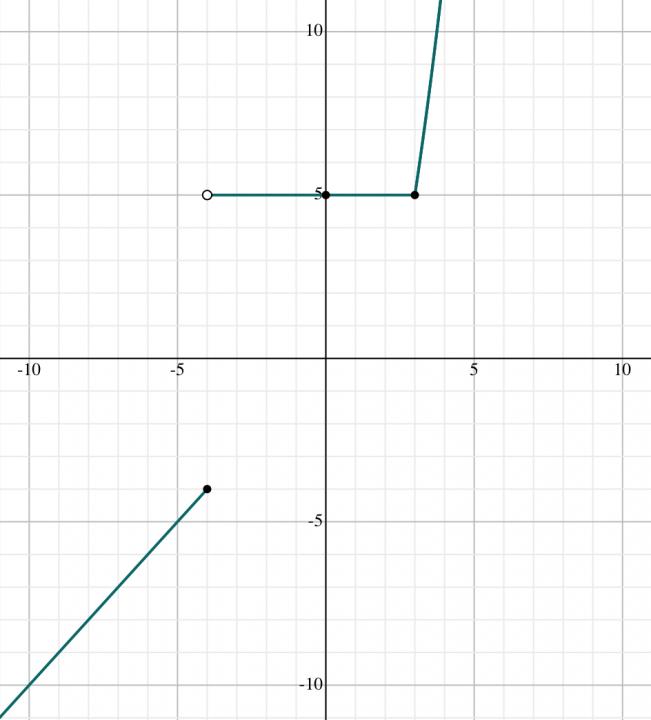
1A:
lim of f(x) as x approaches 3 from the left = 5
lim of f(x) as x approaches 3 from the right = 3² - 4 = 5
The two-sided limit as x approaches 3 is 5.
1B:
lim of f(x) as x approaches -4 from the left = -4
lim of f(x) as x approaches -4 from the right = 5
-4 ≠ 5, therefore it’s discontinuous at x = -4 because the two-sided limit doesn’t exist. It’s also discontinuous because there’s both a hole and a jump at x = -4.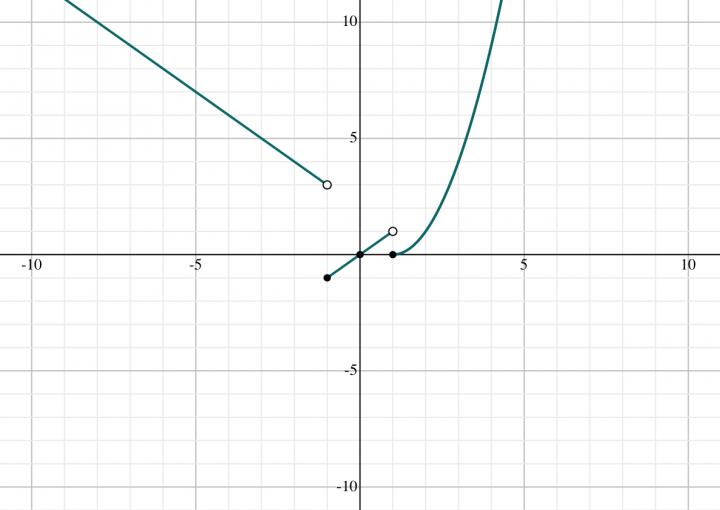
2A:
2 - -1 = 3
lim of f(x) as x approaches -1 from the left is 3
2B:
2 - -1 = 3
-1
3 ≠ -1, therefore the two-sided limit as x approaches -1 doesn’t exist.
2C:
lim of f(x) as x approaches -1 from the right is -1
2D:
0
0
The two-sided limit as x approaches 0 is 0
2E:
1
lim f(x) as x approaches 1 from the left is 1
2F:
1
(1 - 1)² = 0
1 ≠ 0, therefore the two-sided limit as x approaches 1 doesn’t exist.
2G:
(1 - 1)² = 0
lim of f(x) as x approaches 1 from the right is 0
2H:
0

1:
(8 choose 5)(3x)⁵(-2)³
coefficient of x⁵ = 56 x 243 x -8
FINAL ANSWER: -108864
2:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 = (5a)⁷(b)⁰
7 = (5a)⁶(b)¹
21 = (5a)⁵(b)²
35 = (5a)⁴(b)³
35 = (5a)³(b)⁴
21 = (5a)²(b)⁵
7 = (5a)¹(b)⁶
1 = (5a)⁰(b)⁷
= 35 x 5³ x a³b⁴
FINAL ANSWER: 4375.
3:
coefficient of a⁵b⁷
(12 choose 5) = (12 choose 7)
FINAL ANSWER: 792
4:
- (512/x18) + (2304/x15) - (4608/x12) + x⁹ + (5376/x⁹) - 18x⁶ - (4032/x⁶) + 144x³ + (2016/x³) - 672
FINAL ANSWER: -672
5:
(3x + 2y)⁴
= (3x)⁴ + (4 choose 1)(3x)²(2y) + (4 choose 2)(3x)²(2y)² + (4 choose 3)(3x)(2y)³ + (2y)⁴
FINAL ANSWER: 81x⁴ + 216x³y +216x²y² + 96xy³ + 16y⁴
6A:
(1 +1)⁴
= 2⁴
= 1 + (4 choose 1)(1) + (4 choose 2)(1²) + (4 choose 3)(1³) + 1⁴
⇒ (4 choose 1) + (4 choose 2) + (4 choose 3)
= 16 - 2
FINAL ANSWER: 14
6B:
(1 + 1)⁹
= 1 + (9 choose 1) + (9 choose 2) + (9 choose 3) + (9 choose 4) + (9 choose 5) + (9 choose 6) + (9 choose 7) + (9 choose 8) + 1
⇒ (9 choose 1) + (9 choose 2) + (9 choose 3) + (9 choose 4) + (9 choose 5) + (9 choose 6) + (9 choose 7) + (9 choose 8)
= 2⁹ - 2
FINAL ANSWER: 510
7A:
FINAL ANSWER: 10
7B:
(9 choose 6)3³x⁶(1/x⁶)
FINAL ANSWER: 2268
8:
x³ is in (5 choose 3)(2)²(-x)³
(5 choose 3) = 10
The term is -40x³
FINAL ANSWER: The coefficient is -40.
9:
(7 choose 2)5²(2x²)⁵
FINAL ANSWER: 16800x10
10:
FINAL ANSWER: (2+ax)⁴ = 16 + 32ax + 24a²x² + 8a³x³ + a⁴x⁴
ʃdxdydzUδV + ʃdσU dV/dw - 4 πU’’ = ʃdxdydzVδU + ʃdσV dU/dw - 4 πV’ ….. (3’)
Hmmm. Sort of worked, though the integral signs are a bit stunted.
So, what does it do? I will hazard a guess....
(she took the relevant driving-lessons driving lessons her HGV licence license)
Good points, the differences in spelling based on countries. I had not taken into consideration that you are not here in the US.
For me, anything written in the English language is always about the English language; the two cannot ever be separated one from the other.
~
You’re welcome.
~